基于调制函数法的分数阶系统参数辨识

　　摘 要：调制函数法已经被用于线性和非线性系统的辨识。在这篇文章中，我们将调制函数法推广到分数阶系统的在线辨识中。首先，给出一个基于调制函数的分数阶微分的分部积分公式。然后，我们将这一公式应用到分数阶系统中，将系统输入和输出的分数阶微分转换为调制函数的分数阶微分，通过选取一组调制函数，将分数阶系统参数辨识问题转化为求解代数方程组的问题。

　　关键词：辨识;分数阶系统;调制函数

　　1 概述

　　分数阶微积分方程因为能够准确描述自然世界的现象而得到广泛的应用。多孔介质中的流体运动，半无限平板中的热传导，半无限输电线路的电压电流关系等问题都可以准确地利用分数阶微积分方程描述。该论文主要解决分数阶动力系统的辨识问题，系统辨识的主要目标是根据系统的输入和输出来确定模型参数。在解决分数阶系统辨识问题中已经提出了许多方法，这些方法都是基于整数阶系统辨识方法的推广。我们将这些方法分为时域辨识法和频域辨识法。时域辨识发主要基于利用分数阶微分的 Grunwald 定义将分数阶微分方程进行离散化，并且通过最小二乘法进行参数辨识。文献提出通过有理模型来近似分数阶积分算子。文献利用分数阶正交基函数进行系统辨识。

　　在本文中，我们利用调制函数法进行分数阶系统的参数辨识。调制函数法最早由 Shinbrot 提出来估计状态空间方程中的参数。由于调制函数的性质，由分数阶微分方程表示的分数阶系统可以转化为线性代数方程组。因此这就避免了，在分数阶系统辨识中初始条件的未知对辨识过程的影响。调制函数法在文献中就被推广到分数阶系统辩识问题中，然而该作者仅用该方法降低了分数阶系统中的阶次。

　　在下一节中，我们先回顾分数阶微分和调制函数的定义。然后在第三部分中应用调制函数来辨识分数阶线性系统。仿真实验在第四部分中进行。第五部分进行主要结果的总结。

　　2 预备知识

　　2.1 Riemann-Liouville 分数阶微分

　　设 f 是定义在 R 上的连续函数，那么 f 的 Riemann-Liouville 分数阶微分定义为：

　　(1)这里 ，并且 是 Gamma函数。例如，利用(1)式，n 次多项式的分数阶微分为[7]：

　　2.2 调制函数设 ，g 是一个函数，满足下面性质：那么 g 为 l 阶调制函数。

　　2.3 分数阶分部积分法

　　调制函数的另一个有用的性质由下面定理给出：

　　定理 1：设 y 为一个函数，其 阶分数阶微分存在，并且 g 为 l 阶调制函数， 。

　　3 分数阶系统辨识

　　我们考虑如下分数阶线性系统：

　　这里 y 是输出，u 是输入，ai， 是待辨识的未知参数，并且 ， 满足 ，， 。令 ， ，并且 ，这里 代表大于或等于 的最小整数。然后，我们选取一组调制函数 ，其中 。根据定理 1，我们可以给出下面的引理。

　　引理 2.：令 是一组 l 阶调制函数。我们假设分数阶线性系统(3)中的 ，那么可以通过求解下面的线性系统来对辨识分数阶系统中的未知参数。(4)这 里 ， 为 待 辨 识 参数，并且以及证明：在(3)式两边同乘上 gn 并且在区间 上积分，我们得到：利用定理 1，可以得到(5)定理证毕。

　　通过使用定理 1，可以通过计算调制函数的分数阶微分来代替计算输入和输出函数的分数阶微分。一方面，相比较于输出函数，调制函数是已知的并且不含噪声的。另一方面，有的时候输入函数是非连续函数，这就给计算输入函数的分数阶微分带来很大困难，我们可以通过计算调制函数的分数阶积微分来避免这一困难。最后需要提到的是,在计算(5)式中的积分时，我们采用数值积分方法中的梯形准则。在辨识过程中，如果我们将 T 的值取作辨识参数的时间就可以实现在线辨识。

　　4、 数值实验

　　下面我们利用数值实验来展示本文中辨识方法的准确性与稳定性。

　　我们考虑下面的分数阶系统：在辨识过程中，为了方便计算分数阶微分，我们选取调制函数为 这里取 。选取输入函数为

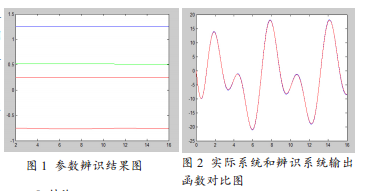
　　并且，利用梯形准则来计算(5)式中的积分。图 1 展示了我们得到的参数辨识结果，图 2 展示了辨识系统的输出和系统真实输出是完全吻合的。

　　5、结论

　　在本论文中，调制函数法被应用到分数阶系统的在线辨识中。利用该方法，通过求解线性方程组完成分数阶系统辨识问题。由于调制函数的性质，我们避免了计算输入和输出函数的分数阶微分，也可以避免分数阶系统初始条件对辨识过程的影响。方法的有效性和可行性已通过数值算例证实。需要提到的是，该方法依赖于调制函数的选择，今后还需进一步考虑在分数阶时滞系统中未知阶次的辨识问题

　　参考文献

　　[1]A. Oustaloup, L. Le Lay and B. Mathieu, Identification of non integer order system in the time domain, in proceeding IEEE CESA’96, SMCIMACS Multiconference, Computational En- gineering in Systems Application, Symposium on Control, Opti- misation and Supervision, Lille, France, July 9-12,1996.

　　[2] J.C. Trigeassou, T. Poinot, J.Lin, A. Oustaloup and F. Lev- ron, Modeling and identification of a non integer order system, in: Proceedings of the ECC99, European Control Conference, Karlsruhe, Germany, 1999.

　　推荐阅读：高等数学教学措施应用

《基于调制函数法的分数阶系统参数辨识》

上一篇：太阳能电池中具有 D － A － π － A 型有机染料分子的理论研究

下一篇：水面舰艇对抗线导鱼雷的现状分析